Vés al contingut

Entrenament i validació de conjunts de dades

De la Viquipèdia, l'enciclopèdia lliure
Principis de l'aprenentatge automàtic.

En l'aprenentatge automàtic, una tasca habitual és l'estudi i la construcció d'algorismes que puguin aprendre i fer prediccions sobre les dades.[1] Aquests algorismes funcionen fent prediccions o decisions basades en dades,[2] mitjançant la construcció d'un model matemàtic a partir de dades d'entrada. Aquestes dades d'entrada que s'utilitzen per construir el model solen dividir-se en diversos conjunts de dades. En particular, s'utilitzen habitualment tres conjunts de dades en diferents etapes de la creació del model: formació, validació i conjunts de proves.

El model s'ajusta inicialment a un conjunt de dades d'entrenament,[3] que és un conjunt d'exemples utilitzats per ajustar els paràmetres (per exemple, els pesos de les connexions entre neurones en xarxes neuronals artificials) del model.[4] El model (per exemple, un classificador Bayes ingenu) s'entrena en el conjunt de dades d'entrenament mitjançant un mètode d'aprenentatge supervisat, per exemple utilitzant mètodes d'optimització com ara el descens del gradient o el descens del gradient estocàstic. A la pràctica, el conjunt de dades d'entrenament sovint consta de parells d'un vector d'entrada (o escalar) i el vector de sortida corresponent (o escalar), on la clau de resposta es denota habitualment com a objectiu (o etiqueta). El model actual s'executa amb el conjunt de dades d'entrenament i produeix un resultat, que després es compara amb l' objectiu, per a cada vector d'entrada del conjunt de dades d'entrenament. A partir del resultat de la comparació i de l'algorisme d'aprenentatge específic que s'utilitza, s'ajusten els paràmetres del model. L'ajustament del model pot incloure tant la selecció de variables com l'estimació de paràmetres.

Un conjunt d'entrenament (esquerra) i un conjunt de proves (dreta) de la mateixa població estadística es mostren com a punts blaus. Dos models predictius s'ajusten a les dades d'entrenament. Els dos models equipats es representen amb els conjunts d'entrenament i de prova. Al conjunt d'entrenament, el MSE de l'ajust que es mostra en taronja és 4, mentre que el MSE de l'ajust que es mostra en verd és 9. Al conjunt de proves, el MSE de l'ajust que es mostra en taronja és 15 i el MSE de l'ajust que es mostra en verd és 13. La corba taronja sobrepassa greument les dades d'entrenament, ja que el seu MSE augmenta gairebé un factor de quatre quan es compara el conjunt de proves amb el conjunt d'entrenament. La corba verda sobreajusta les dades d'entrenament molt menys, ja que el seu MSE augmenta menys d'un factor de 2.

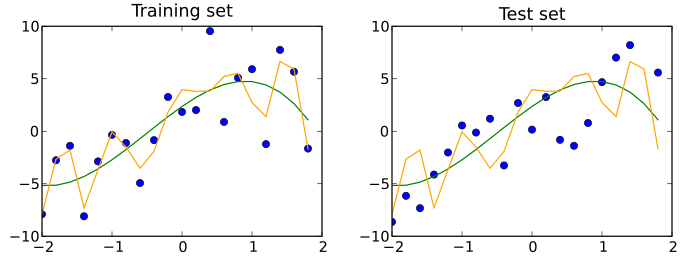
Successivament, el model ajustat s'utilitza per predir les respostes de les observacions en un segon conjunt de dades anomenat conjunt de dades de validació.[5] El conjunt de dades de validació proporciona una avaluació imparcial de l'ajust d'un model al conjunt de dades d'entrenament mentre s'ajusten els hiperparàmetres del model [6] (per exemple, el nombre d'unitats ocultes (capes i amplades de capes) en una xarxa neuronal [7]). Els conjunts de dades de validació es poden utilitzar per a la regularització mitjançant una aturada anticipada (aturant l'entrenament quan augmenta l'error del conjunt de dades de validació, ja que això és un signe d'adaptació excessiva al conjunt de dades d'entrenament).[8] Aquest procediment senzill es complica a la pràctica pel fet que l'error del conjunt de dades de validació pot fluctuar durant l'entrenament, produint múltiples mínims locals. Aquesta complicació ha portat a la creació de moltes regles ad-hoc per decidir quan ha començat realment el sobreajustament.[8]

Referències

[modifica]
  1. ↑ Ron Kohavi; Foster Provost Machine Learning, 30, 1998, pàg. 271–274. DOI: 10.1023/A:1007411609915 [Consulta: free].
  2. ↑ Bishop, Christopher M. Pattern Recognition and Machine Learning (en anglès). New York: Springer, 2006, p. vii. ISBN 0-387-31073-8. 
  3. ↑ James, Gareth. An Introduction to Statistical Learning: with Applications in R (en anglès). Springer, 2013, p. 176. ISBN 978-1461471370.  Arxivat 2019-06-23 a Wayback Machine.
  4. ↑ Ripley, Brian. Pattern Recognition and Neural Networks. Cambridge University Press, 1996, p. 354. ISBN 978-0521717700. 
  5. ↑ James, Gareth. An Introduction to Statistical Learning: with Applications in R (en anglès). Springer, 2013, p. 176. ISBN 978-1461471370.  Arxivat 2019-06-23 a Wayback Machine.
  6. ↑ Brownlee, Jason. «What is the Difference Between Test and Validation Datasets?» (en anglès), 13-07-2017. [Consulta: 12 octubre 2017].
  7. ↑ Ripley, Brian. Pattern Recognition and Neural Networks (en anglès). Cambridge University Press, 1996, p. 354. ISBN 978-0521717700. 
  8. ↑ 8,0 8,1 Prechelt, Lutz. «Early Stopping — But When?». A: Grégoire Montavon. Neural Networks: Tricks of the Trade (en anglès). Springer Berlin Heidelberg, 2012, p. 53–67 (Lecture Notes in Computer Science). DOI 10.1007/978-3-642-35289-8_5. ISBN 978-3-642-35289-8. 
Obtingut de «https://ca.wikipedia.org/w/index.php?title=Entrenament_i_validació_de_conjunts_de_dades&oldid=32246536»